Assalamu’alaikum WR. WB., pada kesempatan
kali ini saya akan melanjutkan postingan saya sebelumnya yaitu tentang pengenalan game theory. Pada postingan ini saya akan menjelaskan
tentang unsr – unsur dasar yang ada di dalam game theory. Langsung saja kita
lihat apa saja unsur – unsur dasar yang ada di dalamnya.
Ada beberapa unsur atau konsep dasar yang sangat penting dalam penyelesaian
setiap kasus dengan teori permainan. Berikut penjelassan selengkapnya :
a). Jumlah Pemain
 |
| Jumlah Pemain |
Permainan diklasifikasikan menurut jumlah kepentingan atau tujuan yang ada dalam permainan tersebut. Dalam hal ini perlu dipahami, bahwa pengertian “jumlah pemain” tidak selalu sama artinya dengan “jumlah Orang” yang terlibat dalam permainan. jumlah pemain disini berarti jumlah kelompok pemain berdasarkan masing-masing kepentingan atau tujuannya. Dengan demikian dua orang atau lebih yang mempunyai kepentingan yang sama dapat diperhitungkan sebagai satu kelompok pemain.
b). Ganjaran
/ Pay-off
 |
| Pay Off (Ganjaran) |
Ganjaran / pay-off adalah hasil akhir yang terjadi pada
akhir permainan berkenaan dengan ganjaran ini, permainan digolongkan menjadi 2
macam kategori, yaitu permainan jumlah-nol (zero-sum games) dan
permainan jumlah-bukan-nol (non-zero-sum games).
permainan jumlah-nol terjadi jika jumlah ganjaran dari seluruh pemain adalah
nol, yaitu dengan memperhitungkan setiap keuntungan sebagai bilangan positif
dan setiap kerugian sebagai bilangan negatif. Selain dari itu adalah permainan
jumlah – bukan-nol. Dalam permainan jumlah-nol setiap kemenangan bagi suatu
pihak pemain merupakan kekalahan bagi pihak pemain lain. letak arti penting
dari perbedaan kedua kategori permainan berdasarkan ganjaran ini adalah bahwa
permainan jumlah-nol adalah suatu sistem yang tertutup. Sedangkan permainan
jumlah-bukan-nol tidak demikian halnya. Hampir semua permainan pada dasarnya
merupakan permainan jumlah-nol. Berbagai situasi dapat dianalisis sebagai
permainan jumlah-nol.
c). Strategi Permainan
 |
| Strategi Permainan |
Strategi
permainan dalam teori permainan adalah suatu siasat atau rencana tertentu dari
seorang pemain, sebagai reaksi atas aksi yang mungkin dilakukan oleh pemain
yang menjadi saingannya. permainan diklasifikasikan menurut jumlah strategi
yang tersedia bagi masing-masing pemain. Jika pemain pertama memiliki m kemungkinan
strategi dan pemain kedua memiliki n kemungkinan strategi, maka permainan
tersebut dinamakan permainan m x n. letak arti penting dari perbedaan jenis
permainan berdasarkan jumlah strategi ini adalah bahwa permainan dibedakan
menjadi permainan berhingga dan permainan tak berhingga. Permainan berhingga
terjadi apabila jumlah terbesar dari strategi yang dimiliki oleh setiap pemain
berhingga atau tertentu, sedangkan permainan tak berhingga terjadi jika
setidak-tidaknya seorang pemain memiliki jumlah strategi yang tak berhingga
atau tidak tertentu.
d). Matriks Permainan
Setiap permainan yang dianalisis dengan
teori permainan selalu dapat disajikan dalam bentuk sebuah matriks permainan.
matriks permainan disebut juga matriks ganjaran yaitu sebuah matriks yang semua
unsur berupa ganjaran dari para pemain yang terlibat dalam permainan tersebut.
Baris-barisnya melambangkan strategi –strategi yang dimiliki pemain pertama,
sedangkan kolom-kolomnya melambangkan strategi-strategi yang dimiliki pemain
lain. dengan demikian, permainan berstrategi mxn dilambangkan dengan matriks
permainan m x n . Teori permainan berasumsi bahwa strategi yang tersedia bagi
masing-masing pemain dapat dihitung dan ganjaran yang berkaitan dengannya dapat
dinyatakan dalam unit, meskipun tidak selalu harus dalam unit moneter. Hal ini
penting bagi penyelesaian permainan, yaitu untuk menentukan pilihan strategi
yang akan dijalankan oleh masing-masing pemain, dengan menganggap bahwa masing
masing pemain berusaha memaksimumkan keuntungannya yang minimum (maksimin) atau
meminimumkan kerugiannya yang maksimum (minimaks). Nilai dari suatu permainan
adalah ganjaran rata-rata / ganjaran yang diharapkan dari sepanjang rangkaian
permainan, dengan menganggap kedua pemain selalu berusaha memainkan strateginya
yang optimum. Secara konvensional, nilai permainan dilihat dari pihak pemain
yang strategistrateginya dilambangkan oleh baris-baris matriks ganjaran, dengan
kata lain dilihat dari sudut pandang pemain tertentu. pemain dikatakan adil (fair) apabila nilainya nol, dimana takseorang pemain
pun yang memperoleh keuntungan atau kemenangan dalam permainan yang tidak adil
(unfair) seorang pemain akan memperoleh kemenangan atas
pemain lain, yaitu jika nilai permainan tersebut bukan nol, dalam hal ini nilai
pemain adalah positif jika pemain pertam (pemain baris) memperoleh kemenangan,
sebaliknya nilai permainan negatif jika pemain lain (pemain kolom) memperoleh
kemenangan.
e). Titik
Pelana (Saddle Poin)
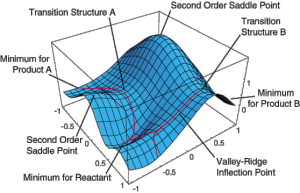 |
| Titik Pelana |
Titik pelana adalah suatu unsur didalam
matriks permainan yang sekaligus sebagai maksimin baris dan minimaks kolom.
permainan dikatakan bersaing ketat (Strictly determined)
jika matriksnya memiliki titik pelana. Strategi yang optimum bagi masing-masing
pemain adalah strategi pada baris dan kolom yang mengandung titik pelana
tersebut. dalam hal ini baris yang mengandung titik pelana merupakan strategi
optimum bagi pemain pertama, sedangkan kolom yang mengandung titik pelana
merupakan strategi optimum bagi pemain lain. Langkah pertama penyelesaian sebuah
matriks permainan adalah memeriksa ada atau tidaknya titik pelana. Bila
terdapat titik pelana permainan dapat segera dianalisis untuk diselesaikan.
Untuk menentukan titik pelana biasanya dilakukan dengan menuliskan nilai-nilai
minimum dan Maksimum masing-masing kolom, kemudian menentukan maksimun diantara
minimum baris dan minimum diantara maksimum kolom. jika unsur maksimum dari
minimum baris sama dengan unsur minimum dari maksimum kolom, atau jika maksimin
= minimaks, berarti unsur tersebut merupakan titik pelana.
Teori permainan dapat diterapkan dalam
berbagai bidang, meliputi kemiliteran, bisnis, social, ekonomi dan ekologi.
Sebagai contoh pada dunia bisnis, seorang direktur suatu perusahaan didalam
memperkenalkan sebuah produk baru berusaha mengetahui kemungkinan strategi
paling baik atau suatu kombinasi strategi untuk merebut market share yang lebih besar, sementara
saingannya juga mencoba meperkenalkan produk sejenis dengan strategi yang
berbeda dengan direktur pemasaran tersebut, antara lain: penurunan harga,
pemberian hadiah, peningkatan mutu produk, memilih media advertasi yang
efektif. Disinilah peranan teori permainan untuk menentukan strategi mana yang
akan diputuskan oleh dirktur pemasaran tersebut untuk merebut pasar. Persaingan
yang dicontohkan diatas dapat diidentifikasi untuk menjelaskan konsep teori
permainan yang terdiri dari beberapa unsur-unsur dasar, yaitu:
1. Angka-angka dalam matriks pay-off, atau biasa disebut matriks permainan,
menunjukkan hasil-hasil (pay-off) dari
strategi–strategi permainan yang berbeda-beda, hasil-hasil ini dinyatakan dalam
suatu bentuk ukuran efektifitas seperti uang, persentasemarket share, atau utilitas.
2. Maximizing player adalah
pemain yang berada di baris dan yang memenangkan/memperoleh keuntungan
permainan, sedangkan minimizing playeradalah pemain yang berada di kolom dan yang
menderita kekalahan / kerugian.
3.
Strategi permainan adalah rangkaian kegiatan atau rencana yang
menyeluruh dari seorang pemain, sebagai reaksi atas perilaku pesaingnya. Dalam
hal ini, strategi atau rencana tidak dapat dirusak oleh pesaing lainya.
4.
Aturan-aturan permainan adalah pola dimana para pemain memilih
strategi.
5.
Nilai permainan adalah hasil pay-off yang
diperkirakan oleh pemain sepanjang rangkaian permainan dimana masing-masing pemain
menggunakan strategi terbaiknya. Permainan dikatakan adil apabila nilai
permainan sama dengan nol dan sebaliknya.
6.
Dominan adalah kondisi dimana pemain dengan setiap pay-offnya dalam
strategi superior terhadap setiap pay-off yang
berhubungan dalam suatu strategi alternative. Aturan dominan digunakan untuk
mengurangi ukuran matriks pay-off dan
upaya perhitungan.
7.
Strategi optimal adalah kondisi dimana dalam rangkaian kegiatan
permainan seorang pemain berada dalam posisi yang paling menguntungkan tanpa menghiraukan
kondisi pesaingnya.
8.
Tujuan dari model adalah mengidentifikasi strategi atau rencana
optimal untuk setiap pemain.
Demikianlah postingan saya kali ini yaitu tentang unsur – unnsur dalam game theory.. Semoga
postingan saya kali ini dapat berguna serta membuka wawasan kita tentang
pengertian dari game theory khususnya bagi saya dan bagi para pembaca khusunya.
Wassalamu’alaikum WR. WB.










0 komentar:
Posting Komentar